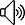Detect Cycle in a Directed Graph

Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false. For example, the following graph contains three cycles 0->2->0, 0->1->2->0 and 3->3, so your function must return true.

Solution
Depth First Traversal can be used to detect cycle in a Graph. DFS for a connected graph produces a tree. There is a cycle in a graph only if there is a  back edge  present in the graph. A back edge is an edge that is from a node to itself (selfloop) or one of its ancestor in the tree produced by DFS. In the following graph, there are 3 back edges, marked with cross sign. We can observe that these 3 back edges indicate 3 cycles present in the graph.

For a disconnected graph, we get the DFS forrest as output. To detect cycle, we can check for cycle in individual trees by checking back edges.

To detect a back edge, we can keep track of vertices currently in recursion stack of function for DFS traversal. If we reach a vertex that is already in the recursion stack, then there is a cycle in the tree. The edge that connects current vertex to the vertex in the recursion stack is back edge. We have used recStack[] array to keep track of vertices in the recursion stack.

 

        class Graph
{
    int V;    // No. of vertices
    list<int> *adj;    // Pointer to an array containing adjacency lists
    bool isCyclicUtil(int v, bool visited[], bool *rs);  // used by isCyclic()
public:
    Graph(int V);   // Constructor
    void addEdge(int v, int w);   // to add an edge to graph
    bool isCyclic();    // returns true if there is a cycle in this graph
};
 
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}
 
void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); // Add w to v’s list.
}
 
// This function is a variation of DFSUytil() in http://www.geeksforgeeks.org/archives/18212
bool Graph::isCyclicUtil(int v, bool visited[], bool *recStack)
{
    if(visited[v] == false)
    {
        // Mark the current node as visited and part of recursion stack
        visited[v] = true;
        recStack[v] = true;
 
        // Recur for all the vertices adjacent to this vertex
        list<int>::iterator i;
        for(i = adj[v].begin(); i != adj[v].end(); ++i)
        {
            if ( !visited[*i] && isCyclicUtil(*i, visited, recStack) )
                return true;
            else if (recStack[*i])
                return true;
        }
 
    }
    recStack[v] = false;  // remove the vertex from recursion stack
    return false;
}
 
// Returns true if the graph contains a cycle, else false.
// This function is a variation of DFS() in http://www.geeksforgeeks.org/archives/18212
bool Graph::isCyclic()
{
    // Mark all the vertices as not visited and not part of recursion
    // stack
    bool *visited = new bool[V];
    bool *recStack = new bool[V];
    for(int i = 0; i < V; i++)
    {
        visited[i] = false;
        recStack[i] = false;
    }
 
    // Call the recursive helper function to detect cycle in different
    // DFS trees
    for(int i = 0; i < V; i++)
        if (isCyclicUtil(i, visited, recStack))
            return true;
 
    return false;
}
 
int main()
{
    // Create a graph given in the above diagram
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);
 
    if(g.isCyclic())
        cout << "Graph contains cycle";
    else
        cout << "Graph doesn't contain cycle";
    return 0;
}
      

 

 

Time Complexity of this method is same as time complexity of  DFS traversal  which is O(V+E).

 

Reference:

http://www.geeksforgeeks.org/detect-cycle-in-a-graph/