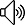Jensen不等式
Jensen不等式给出了积分的凸函数值必定大于凸函数(convex)的积分值的定理。在凸函数曲线上的任意两点间连接一条线段，那么线段会位于曲线之上，这就是将Jensen不等式应用到两个点的情况，如图(1)所示\((t\in[0,1])\)。我们从概率论的角度来描述Jensen不等式：假设\(f(x)\)为关于随机变量\(x\)的凸函数\(f'(x)\geq 0\)，则有\(f\left(E(x)\right)\leq E\left(f(x)\right)\)。反之，如果\(f(x)\)为关于\(x\)的凹函数(concave)，则有\(f\left(E(x)\right)\geq E\left(f(x)\right)\)。
对于严格的凸函数\(\left(f''(x)>0\right)\)，想取得相等关系\(f\left(E(x)\right)=E\left(f(x)\right)\)，则有\(x=E(x)\)，那么\(x\)必须为常数。
期望最大化
期望最大化(Expectation Maximization,EM)算法常用于求解概率模型的极大似然问题，其典型的应用场景包括：1)观察到的数据不完全;2)似然函数无法直接计算但可以用隐变量(latent variables)来表示。对于第一种应用场景，我们可以将缺失的数据视为隐变量，然后用已有的观测数据将其推导出来，最后也就回到了第二种应用场景。假设在概率模型中，\(x^{(i)}\)和\(z^{(i)}\)分别为观测值和隐变量(\(i=1,2,\cdots,m\))，两者的联合概率为\(p(x,z;\theta)\)，其中\(\theta\)为模型参数。我们的目标是在仅知道\(x^{(i)}\)的前提下，求最佳的模型参数\(\theta\)以最大化似然函数 \begin{equation} \mathcal{L}(\theta)=\sum_{i=1}^m\log\left(x^{(i)};\theta\right)=\sum_{i=1}^m\log\sum_{j=1}^Kp\left(x^{(i)},z^{(i)}=j;\theta\right) \end{equation} 这里简单假设\(z^{(i)}\)为离散值\(\{1,2,\cdots,K\}\)，在\(z^{(i)}\)为连续值或离散值和连续值的组合时情况也是类似的。 在仅知道\(x^{(i)}\)的情况下用极大似然法估计参数很困难。如果\(z^{(i)}\)只可能取少数几个离散值，我们还可以根据\(z^{(i)}\)分情况优化似然函数，最终求得最合理的模型参数；但若\(z^{(i)}\)的取值情况很复杂时，前面的方法很显然是行不通的。既然直接求解似然函数的最大值很难，只能退而求其次，求似然函数下界的最大值，得到一个相对较好的模型参数，这就是EM算法的精髓所在。这里我们引入隐变量\(z^{(i)}\)的概率分布\(Q_i(z^{(i)})\)，则对数似然函数表述为如下形式： \begin{equation} \begin{array}{rl} \mathcal{L}(\theta)&=\sum_{i=1}^m\log\sum_{z^{(i)}=1}^KQ_i\left(z^{(i)}\right)\frac{p\left(x^{(i)},z^{(i)};\theta\right)}{Q_i\left(z^{(i)}\right)}\\ &=\sum_{i=1}^m\log E_{z^{(i)}\sim Q_i}\left[\frac{p\left(x^{(i)},z^{(i)};\theta\right)}{Q_i\left(z^{(i)}\right)}\right] \end{array} \end{equation} \(Q_i(z^{(i)})\)为隐变量\(z^{(i)}\)的概率分布，必须满足约束条件： \begin{equation} Q_i(z^{(i)})\geq 0,\sum_{z^{(i)}=1}^KQ_i(z^{(i)})=1 \end{equation} 对数函数\(\log x\)在区间\((0,+\infty)\)上为严格的凹函数，根据Jensen不等式可得到似然函数的下界： \begin{equation} \begin{array}{rl} \mathcal{L}(\theta)&=\sum_{i=1}^m\log E_{z^{(i)}\sim Q_i}\left[\frac{p\left(x^{(i)},z^{(i)};\theta\right)}{Q_i\left(z^{(i)}\right)}\right]\\ &\geq \sum_{i=1}^mE_{z^{(i)}\sim Q_i}\left[\log \frac{p\left(x^{(i)},z^{(i)};\theta\right)}{Q_i\left(z^{(i)}\right)}\right]=L(\theta) \end{array} \end{equation}
从EM算法的描述可知，EM算法的每次迭代分为两步：E-step和M-step，如图(2)所示。
E-step使似然函数下界\(L(\theta)\)在\(\theta^{(t)}\)处紧贴着似然函数\(\mathcal{L}(\theta)\)，我们需要调整\(Q_i(z^{(i)})\)以满足： \begin{equation} \frac{p\left(x^{(i)},z^{(i)};\theta\right)}{Q_i\left(z^{(i)}\right)}=C \end{equation} 结合\(Q_i(z^{(i)})\)的约束条件，很容易得到如下关系式： \begin{equation} Q_i(z^{(i)})=\frac{p\left(x^{(i)},z^{(i)};\theta\right)}{\sum_{z^{(i)}=1}^K p\left(x^{(i)},z^{(i)};\theta\right)}=\frac{p\left(x^{(i)},z^{(i)};\theta\right)}{p\left(x^{(i)};\theta\right)}=p\left(z^{(i)}|x^{(i)};\theta\right) \end{equation} M-step则求使\(L(\theta^{(t)})\)取得极大值的参数\(\theta^{(t+1)}\)作为下一次迭代的初始点。
如果将\(L(\theta)\)定义为关于\(Q_i(z^{(i)})\)和\(\theta\)的函数\(J(Q,\theta)\)，则EM算法的优化策略和坐标上升(coordinate ascent)是一致的。在E-step中，沿着\(Q\)定义的方向最大化\(J(Q,\theta)\)；在M-step中，沿着\(\theta\)定义的方向最大化\(J(Q,\theta)\)，这也可以解释EM算法在迭代过程中会使目标函数收敛到局部最优解。
高斯混合模型
密度估计(Density Estimation)中的高斯混合模型（Gaussian Mixture Model,GMM)是EM算法的一个典型应用，下面就以GMM为例展示EM的强大威力。高斯混合模型可以表示成\(K\)个高斯分布的线性加权： \begin{equation} P(x)=\sum_{k=1}^K\phi_k\mathcal{N}(x|\mu_k,\Sigma_k) \end{equation} 其中\(w_k\)为第\(k\)个高斯分布的权值。我们要估算出模型中的所有参数\(\phi_k,\mu_k,\Sigma_k\)。 假设现有观测数据集合\(\mathcal{S}=\{x^{(i)}|x^{(i)}\in\mathbb{R}^n,i=1,\cdots,m\}\)，每个样本\(x^{(i)}\)都有一个对应的隐变量\(z^{(i)}\in\{1,\cdots,K\}\)表示\(x^{(i)}\)属于哪一个高斯分布,\(z^{(i)}\)服从参数为\(\phi_1,\cdots,\phi_K\)的多项分布\(P(z^{(i)}=k)=\phi_k\)，参数满足以下约束条件： \begin{equation} \sum_{k=1}^K\phi_k=1,\quad \phi_k\geq 0,k=1,\cdots,K \end{equation} \(x^{(i)}\)和\(z^{(i)}\)之间的联合分布\(P(x^{(i)},z^{(i)})=P(x^{(i)}|z^{(i)})P(z^{(i)})\)。在已知\(z^{(i)}=k\)的前提下我们知道\(x^{(i)}\)的概率分布，即\(x^{(i)}|z^{(i)}\sim \mathcal{N}(\mu_k,\Sigma_k)\): \begin{equation} P(x^{(i)}|z^{(i)}=k)=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma_k|^{\frac{1}{2}}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu_k)^T\Sigma_k^{-1}(x^{(i)}-\mu_k)\right) \end{equation} 很可惜\(z^{(i)}\)是未知的隐变量，可能是任意一个高斯分布，因此\(P(x^{(i)})=\sum_{z^{(i)}=1}^K P(x^{(i})|z^{(i)})P(z^{(i)})\)。似然函数形式如下： \begin{equation} \ell({\phi,\mu,\Sigma})=\prod_{i=1}^mP(x^{(i)};\phi,\mu,\Sigma)=\prod_{i=1}^m\left(\sum_{z^{(i)}=1}^K P(x^{(i}|z^{(i)})P(z^{(i)})\right) \end{equation} 将上式转化为形式上更简单的对数似然函数并加上约束条件构成拉格郎日函数： \begin{equation} \mathcal{L}({\phi,\mu,\Sigma})=\sum_{i=1}^m\log\left(\sum_{z^{(i)}=1}^K P(x^{(i}|z^{(i)})P(z^{(i)})\right)+\lambda(\sum_{k=1}^K\phi_k-1) \end{equation} 仔细观察这个拉格郎日函数，我们发现对数函数的输入为多个高斯函数的加权，这就导致了利用普通的求偏导方法是无法获得一个解析解的。根据前面的EM算法，我们先执行E-step，利用贝叶斯定律猜测每个样本服从每个高斯分布的概率： \begin{equation} Q_k^{(i)}=P(z^{(i)}=k|x^{(i)})=\frac{P(x^{(i)}|z^{(i)}=k)P(z^{(i)}=k)}{\sum_{k=1}^KP(x^{(i)}|z^{(i)}=k)P(z^{(i)}=k)} \end{equation} 然后求得与上述拉格郎日函数等价的下界函数\(L(\phi,\mu,\Sigma)\): \begin{equation} \begin{array}{rl} L(\phi,\mu,\Sigma)&=\sum_{i=1}^m\sum_{k=1}^KQ_k^{(i)}\log P(x^{(i)},z^{(i)}=k)+\lambda(\sum_{k=1}^K\phi_k-1)\\ &=\sum_{i=1}^m\sum_{k=1}^KQ_k^{(i)}\left(\log P(x^{(i)}|z^{(i)}=k)+\log P(z^{(i)}=k)\right)\\ &\quad+\lambda(\sum_{k=1}^K\phi_k-1) \end{array} \end{equation} 注意到该下界函数中的对数函数已经直接作用到每个高斯分布上了。现在我们可以对参数求偏导来计算使下界函数最大的更好的参数。 \begin{equation} \frac{\partial L}{\partial\mu_k}=0\Rightarrow\mu_k=\frac{\sum_{i=1}^mQ_k^{(i)}x^{(i)}}{\sum_{i=1}^mQ_k^{(i)}} \end{equation} \begin{equation} \frac{\partial L}{\partial\Sigma_k}=0\Rightarrow\Sigma_k=\frac{\sum_{i=1}^mQ_k^{(i)}(x^{(i)}-\mu_k)(x^{(i)}-\mu_k)^T}{\sum_{i=1}^mQ_k^{(i)}} \end{equation} \begin{equation} \frac{\partial L}{\partial\phi_k}=0\Rightarrow\sum_{i=1}^m\frac{Q_k^{(i)}}{\phi_k}+\lambda=0 \end{equation} 结合约束条件\(\sum_{k=1}^K\phi_k=1\)，得到\(\lambda=-m\),因此\(\phi_k=\sum_{i=1}^mQ_k^{(i)}/m\)。 根据上述推到，我们给出GMM模型的算法：
EM算法收敛速度要比K-means慢，而且每次迭代的计算量也很大。较好的初始值可以加快收敛速度，因此通常可以用K-means完成粗略的聚类，然后用每个类簇的均值、方差和类簇占总样本的比例来初始化GMM的参数。似然函数可能存在多个局部最优解，且EM算法肯定可以搜索到似然函数的局部最大值，但不能保证可以求得全局的最大值。
根据上述的GMM算法，我写了一个 Python版本的GMM代码 。我随机生成了3组高斯分布的数据，并在图(3)中用三种不同颜色的统计直方图表示；然后用生成的数据用EM算法训练GMM模型，训练过程中的对数似然函数的变化曲线如图(4)所示；最后用训练好的GMM模型反过来预测训练数据的概率密度函数值，如图(3)中的红色曲线所示。
